Bianca Sersante
The interaction between a stellar binary and a Massive Black Hole (MBH) such as Sgr A* in the centre of the Milky Way can result in the disruption of the binary, leading to the ejection of a hypervelocity star (HVS). However, there is a non-zero probability for a binary to survive the encounter. It can end up either unbound from the MBH, or it can remain bound and return to interact again. Robust modelling of the dynamics of persistent binaries and HVSs can allow to map the binary population in the Galactic Centre (GC) and to constrain its origin and assembly history.
Using an analytic approach that consists in treating the system as a restricted 3-body problem, we aim at exploring the fate of a population of circular, eccentric and inclined binaries throughout multiple pericentre passages. In particular, by considering subsequent generations of HVS, we would like to understand if the disruption probability can be enhanced and higher ejection velocities reached. Moreover, we aim at characterising the orbital properties of the binaries that will populate the GC.
By repeating the analysis for realistic rates of injected binaries, we aim to update HVS mock catalogues and compare results with observations of binaries in the Galactic centre from Gaia and WEAVE.
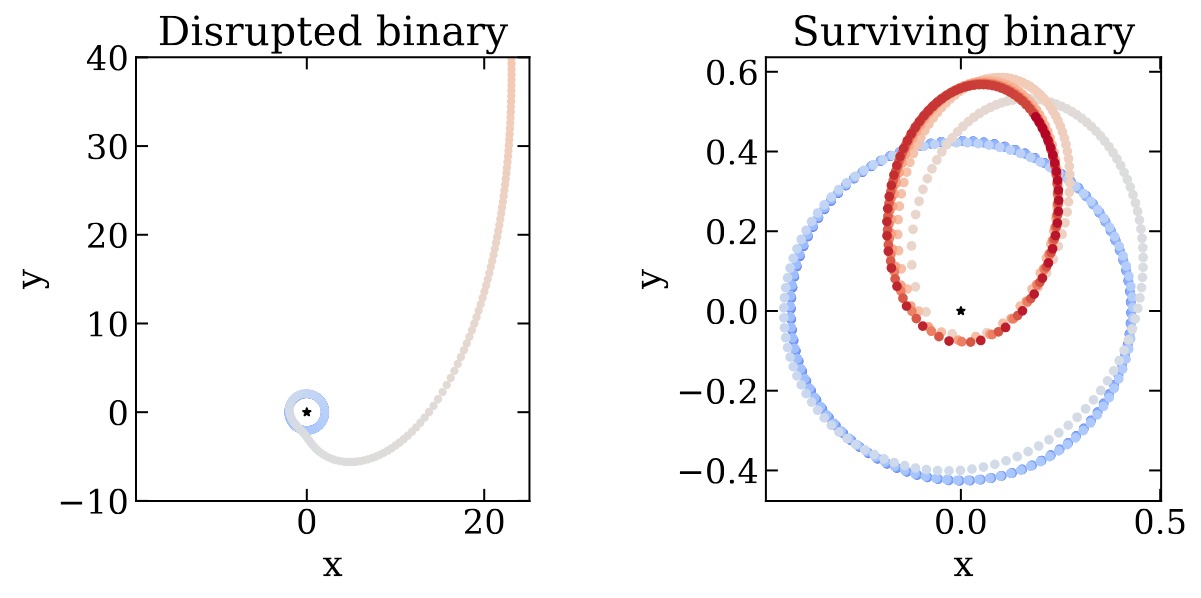
This first figure illustrates two examples of trajectories one of the binary members in the coming frame of the other star (marked with a black star in both panels). Trajectories are coloured with time: blue corresponds to the initial time, white corresponds to the time of closest approach to the BH, and red corresponds to the final time.
In panel (a) we see the trajectory of a binary which is getting disrupted: one of the stars orbits around the other until disruption happens and it is ejected as an HVS.
In panel (b) we see the initial circular trajectory of the star in blue, and, after getting closer to the BH, the binary will survive but now on a different orbit -red one- (the eccentricity and semi-major axis have changed after the interaction with the BH).
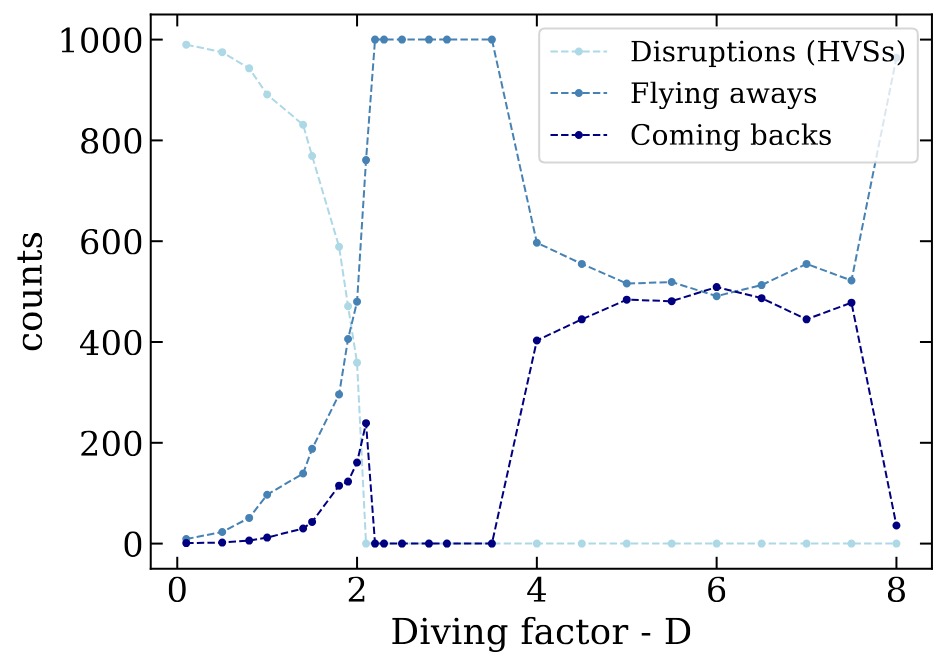
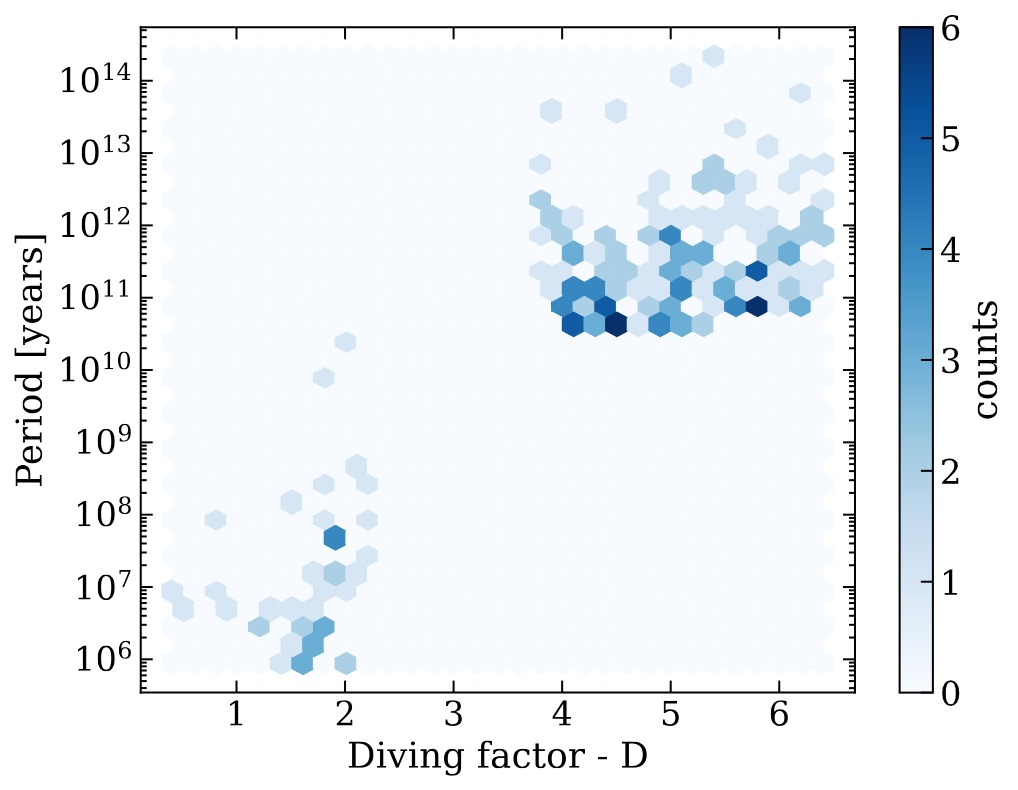
In this second figure, on The x-axis we have the diving factor D. D measures how deeply the binary can dive into the BH tidal sphere – D<1 deep encounters, D>1 shallow encounters. On the y-axis we have the number of binaries that will either be disrupted (light-blue line), or survive and possibly come back (middle blue-line) or fly away (dark-blue line).
For deep encounters, most of the binaries are going to be disrupted (disruption stops at D=2.1). Then, for D between 1.5 and 2.5, there is a fraction of binaries that can interact with the BH again (peak around 2.2). For higher Ds, there is a fraction of binaries that will survive on closed orbits around the BH. However, such orbits are almost hyperbolic. Therefore, in order to understand, among the binaries that survive, which are actually going to interact with the BH, we need to look at the periods.
In this third figure, we are considering only the surviving binaries. P is the time it takes, in years, for a surviving binary to go around the BH again (after the first interaction). In each hexagonal bin, one can read the number of binaries with a given P and a given energy. Only binaries with lower diving factors (deep first encounter) are able to come back with periods smaller than the Hubble time.