Zephyr Penoyre
I work on galactic dynamics through a variety of approaches, with a focus on the galactic centre of our Milky Way, and on hypervelocity stars.
Hypervelocity Stars
The extreme mass and (relatively) small scale of a supermassive black hole (SMBH) like the one at the center of our galaxy leads to incredibly high energy dynamics – close encounters with it can tear objects apart and give the remnant enough velocity to leave the galaxy – we study the (classical) dynamics problems posed by the motion of stars near such an object, particularly of binary stars, whose three body interaction with the SMBH can split the pair, leaving one on a close orbit around the galactic center and the other flying out with huge velocity – these HyperVelocity Stars (HVS) are observable as they make their way out from the galactic center, and thus carry information about that very small and shrouded region into an observable location as well as studying the intricate dynamics of the interaction itself it is important to understand how systems come to be on orbits that come so close to the SMBH – to do this we study the chaotic families of trajectories possible within the center (<100 parsecs) of the galaxy – which are affected by the galactic bulge, nuclear stellar disk and cluster, and the SMBH itself – thus once again linking the properties of the galactic center to an observable output.
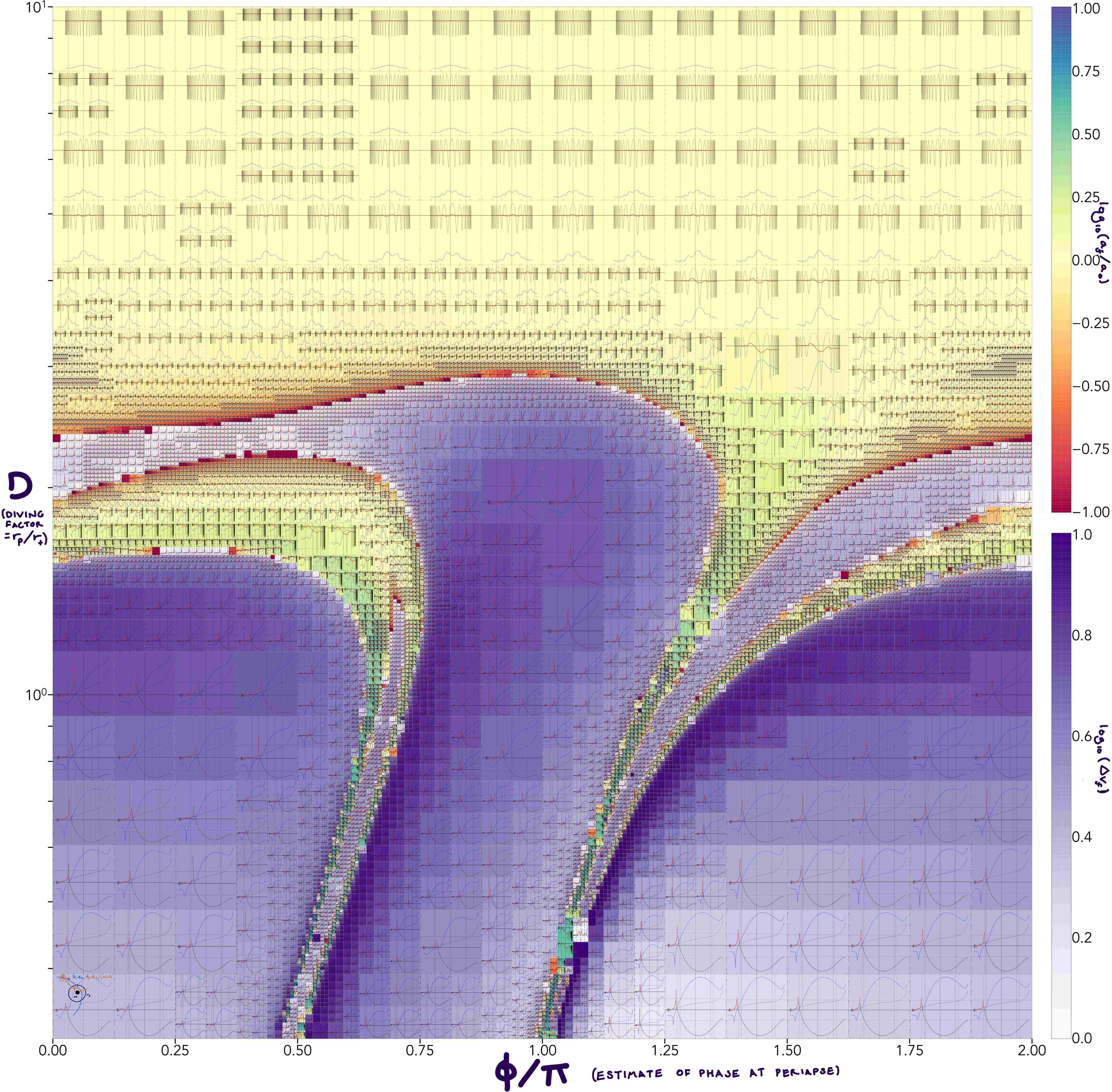
In this figure, a grid of all the possible evolutions and outcomes of an encounter between a binary star (with initial eccentricty of 0.3) and a SMBH, dependant on the diving factor (y-axis, the ratio of the distance of closest approach to the distance at which we’d expect a disruption) and the initial phase of the binary (x-axis) – every subplot shows the evolution of the radius (grey), semi-major axis (red) and eccentricity (blue) throughout the encounter, as a function of time, with the time of closest approach marked as a vertical black line – the color of each subplot shows the ejection velocity (purples) if the binary is disrupted, or the relative change in the size of the binary orbit if the binary survives (reds and oranges show binaries that get tighter, yellow shows binaries that don’t change, and greens and blues show systems where the binary is enlarged).